Introducción
Se utiliza la librería de roboticstoolbox-python para el análisis.
Descargar teoría PDF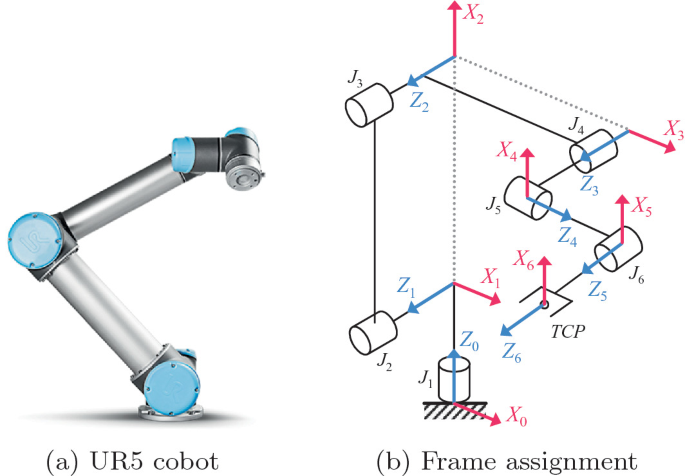
Se utiliza la librería de roboticstoolbox-python para el análisis.
Descargar teoría PDF
import numpy as np
import matplotlib.pyplot as plt
import roboticstoolbox as rtb
from spatialmath import SE3
import matplotlib.pyplot as plt
# Robot UR5 --------------------------------------------------------------
name = "UR5"
print("Robot: ", name, "--------------------------------------------------\n")
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
a3 = 0.3922
a4 = 0.1333
a5 = 0.0997
a6 = 0.0996
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a1, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=-a2, d=0, offset=-np.pi/2, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=-a3, d=0, offset=0, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a4, offset=-np.pi/2, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a5, offset=0, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=0, d=a6, offset=np.pi, qlim=[-2*np.pi, 2*np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi/2, np.pi/2, np.pi/2, np.pi/2, np.pi/2, np.pi/2]
q0 = [t_values[0], t_values[1], t_values[2], t_values[3], t_values[4], t_values[5]]
# Calculate the Jacobian matrix
J = robot.jacob0(q0)
#Asignar valores a las velocidades de las articulaciones
qdot = np.array([0.1, 0.2, 0.3, 0.1, 0.2, 0.3])
# Calcular la velocidad del efector final
v = J @ qdot
'''
Fuerzas y torques
Un 'wrench' del efector final es una representación en seis dimensiones que combina tanto
las fuerzas medidas en N como los momentos (torques) medidos en Nm aplicados en el efector final de un robot.
Se utiliza para modelar y controlar las interacciones del robot con su entorno, permitiendo
regular tanto el movimiento lineal
'''
# Creacion de vector de fureza usando la convencion: [M_x, M_y, M_z, F_x, F_y, F_z]
F = np.array([5, 3, 2, 10, 15, 20])
'''
El método de la transpuesta del Jacobiano es una técnica utilizada en robótica para calcular
los torques en las articulaciones a partir de fuerzas de contacto externas.
El método se basa en la relación entre la fuerza aplicada en el efector final y los torques
resultantes en las articulaciones. La relación se puede expresar matemáticamente como:
Cálculo de torques de las articulaciones:
tau = J(q)^T * F
donde:
- J(q) es la matriz Jacobiana evaluada en la configuración q
- J(q)^T es su transpuesta
- F es el vector de wrench (momentos y fuerzas) aplicado en el efector final
- tau es el vector resultante de torques en las articulaciones
'''
tau = J.T @ F
#imprimir resultados
print("Velocidad Angular (rad/s):")
print("Angular X:", v[0])
print("Angular Y:", v[1])
print("Angular Z:", v[2])
print("\nVelocidad Lineal (m/s):")
print("Lineal X:", v[3])
print("Lineal Y:", v[4])
print("Lineal Z:", v[5])
print("Torques Calculados (Nm):")
for i, t in enumerate(tau, start=1):
print(f"Articulacion {i}: {t:.4f} Nm")
# Robot 1 --------------------------------------------------------------
name = "Esferico 1"
print("Robot: ", name, "--------------------------------------------------\n")
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
a3 = 0.3922
a4 = 0.1333
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=0, a=a2, d=a1, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=a4, d=a3, offset=0 , qlim=[-np.pi, np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi/2, np.pi/2]
q0 = [t_values[0], t_values[1]]
# Calculate the Jacobian matrix
J = robot.jacob0(q0)
#Asignar valores a las velocidades de las articulaciones
qdot = np.array([0.1, 0.2])
# Calcular la velocidad del efector final
v = J @ qdot
# Creacion de vector de fureza usando la convencion: [M_x, M_y, M_z, F_x, F_y, F_z]
F = np.array([5, 3, 2, 10, 15, 20])
tau = J.T @ F
#imprimir resultados
print("Velocidad Angular (rad/s):")
print("Angular X:", v[0])
print("Angular Y:", v[1])
print("Angular Z:", v[2])
print("\nVelocidad Lineal (m/s):")
print("Lineal X:", v[3])
print("Lineal Y:", v[4])
print("Lineal Z:", v[5])
print("Torques Calculados (Nm):")
for i, t in enumerate(tau, start=1):
print(f"Articulacion {i}: {t:.4f} Nm")
# Robot 2 --------------------------------------------------------------
name = "Articulado 2 "
print("Robot: ", name, "--------------------------------------------------\n")
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
a3 = 0.3922
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a1, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=a2, d=0, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=a3, d=0, offset=0 , qlim=[-np.pi, np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi/2, np.pi/2, np.pi/2]
q0 = [t_values[0], t_values[1], t_values[2]]
# Calculate the Jacobian matrix
J = robot.jacob0(q0)
#Asignar valores a las velocidades de las articulaciones
qdot = np.array([0.1, 0.2, 0.3])
# Calcular la velocidad del efector final
v = J @ qdot
# Creacion de vector de fureza usando la convencion: [M_x, M_y, M_z, F_x, F_y, F_z]
F = np.array([5, 3, 2, 10, 15, 20])
tau = J.T @ F
#imprimir resultados
print("Velocidad Angular (rad/s):")
print("Angular X:", v[0])
print("Angular Y:", v[1])
print("Angular Z:", v[2])
print("\nVelocidad Lineal (m/s):")
print("Lineal X:", v[3])
print("Lineal Y:", v[4])
print("Lineal Z:", v[5])
print("Torques Calculados (Nm):")
for i, t in enumerate(tau, start=1):
print(f"Articulacion {i}: {t:.4f} Nm")
# Robot 3 --------------------------------------------------------------
name = "Articulado 3 "
print("Robot: ", name, "--------------------------------------------------\n")
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a1, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=0, offset=0 , qlim=[-np.pi, np.pi]),
rtb.PrismaticDH( alpha=0, a=0, theta=0, offset=a2 , qlim=[-np.pi, np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi/2, np.pi/2, np.pi/2]
q0 = [t_values[0], t_values[1], t_values[2]]
# Calculate the Jacobian matrix
J = robot.jacob0(q0)
#Asignar valores a las velocidades de las articulaciones
qdot = np.array([0.1, 0.2, 0.3])
# Calcular la velocidad del efector final
v = J @ qdot
# Creacion de vector de fureza usando la convencion: [M_x, M_y, M_z, F_x, F_y, F_z]
F = np.array([5, 3, 2, 10, 15, 20])
tau = J.T @ F
#imprimir resultados
print("Velocidad Angular (rad/s):")
print("Angular X:", v[0])
print("Angular Y:", v[1])
print("Angular Z:", v[2])
print("\nVelocidad Lineal (m/s):")
print("Lineal X:", v[3])
print("Lineal Y:", v[4])
print("Lineal Z:", v[5])
print("Torques Calculados (Nm):")
for i, t in enumerate(tau, start=1):
print(f"Articulacion {i}: {t:.4f} Nm")
# Robot 4 --------------------------------------------------------------
name = "Cilindrico 4 "
print("Robot: ", name, "--------------------------------------------------\n")
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
a3 = 0.3922
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.PrismaticDH( alpha=0, a=0, theta=0, offset=a1 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=np.pi/2, a=a2, d=0, offset=0 , qlim=[-np.pi, np.pi]),
rtb.PrismaticDH( alpha=0, a=0, theta=0, offset=a3 , qlim=[-np.pi, np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi/2, np.pi/2, np.pi/2]
q0 = [t_values[0], t_values[1], t_values[2]]
# Calculate the Jacobian matrix
J = robot.jacob0(q0)
#Asignar valores a las velocidades de las articulaciones
qdot = np.array([0.1, 0.2, 0.3])
# Calcular la velocidad del efector final
v = J @ qdot
# Creacion de vector de fureza usando la convencion: [M_x, M_y, M_z, F_x, F_y, F_z]
F = np.array([5, 3, 2, 10, 15, 20])
tau = J.T @ F
#imprimir resultados
print("Velocidad Angular (rad/s):")
print("Angular X:", v[0])
print("Angular Y:", v[1])
print("Angular Z:", v[2])
print("\nVelocidad Lineal (m/s):")
print("Lineal X:", v[3])
print("Lineal Y:", v[4])
print("Lineal Z:", v[5])
print("Torques Calculados (Nm):")
for i, t in enumerate(tau, start=1):
print(f"Articulacion {i}: {t:.4f} Nm")
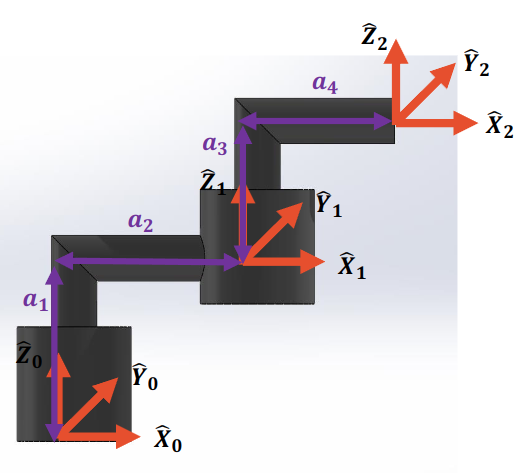
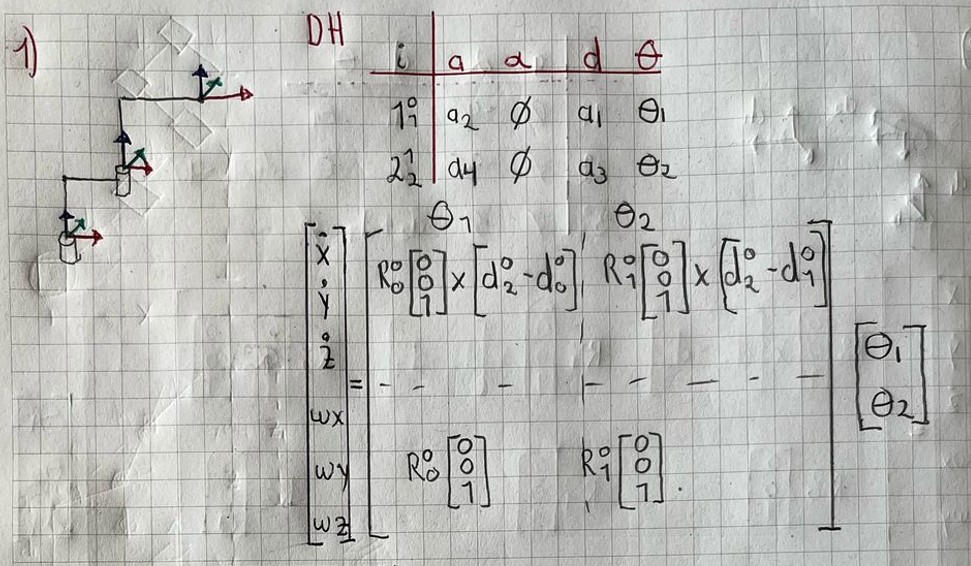
DHRobot: Esférico 1, 2 joints (RR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| q1 | 0.1625 | 0.425 | 0.0° | -180.0° | 180.0° |
| q2 | 0.3922 | 0.1333 | 0.0° | -180.0° | 180.0° |
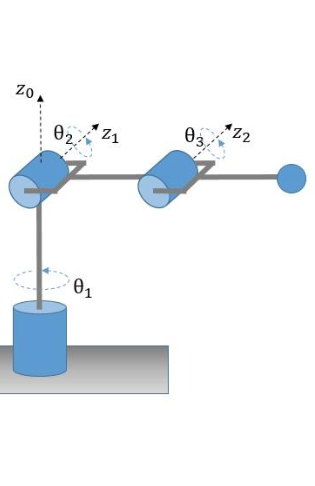

DHRobot: Articulado 2, 3 joints (RRR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| q1 | 0.1625 | 0 | -90.0° | -180.0° | 180.0° |
| q2 | 0 | 0.425 | 0.0° | -180.0° | 180.0° |
| q3 | 0 | 0.3922 | 0.0° | -180.0° | 180.0° |

DHRobot: Articulado 3, 3 joints (RRP), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| q1 | 0.1625 | 0 | -90.0° | -180.0° | 180.0° |
| q2 | 0 | 0 | -90.0° | -180.0° | 180.0° |
| 0.0° | q3 + 0.425 | 0 | 0.0° | -π | π |
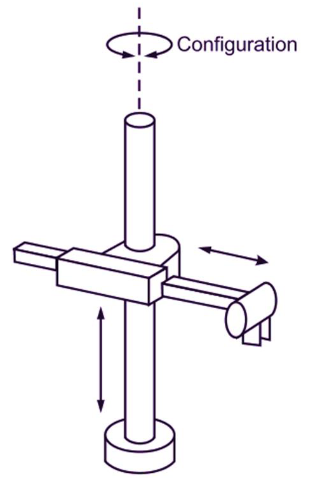
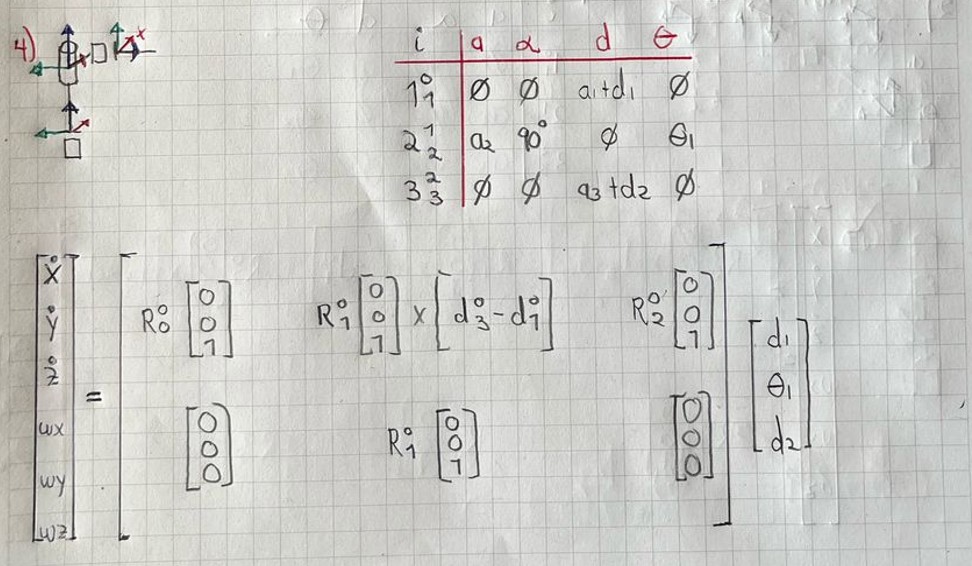
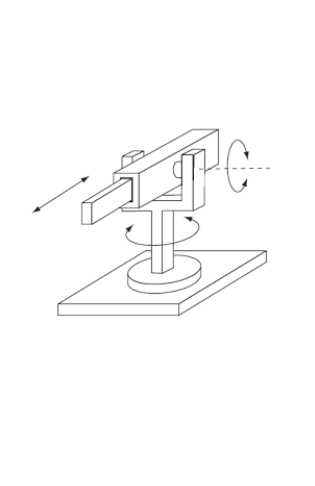
DHRobot: Cilíndrico 4, 3 joints (PRP), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| 0.0° | q1 + 0.1625 | 0 | 0.0° | -π | π |
| q2 | 0 | 0.425 | 90.0° | -180.0° | 180.0° |
| 0.0° | q3 + 0.3922 | 0 | 0.0° | -π | π |