Introducción
Se utiliza la librería de python-roboticstoolbox para el análisis.
Descargar teoría PDF
Se utiliza la librería de python-roboticstoolbox para el análisis.
Descargar teoría PDF
import numpy as np
import matplotlib.pyplot as plt
import roboticstoolbox as rtb
from spatialmath import SE3
import numpy as np
import matplotlib.pyplot as plt
save_path = "Web/Reportes/Teoria/T6/assets"
def inverse_kinematics(robot, Td, q0, ilimit, mask, save_path, name="IK_Solution", status_block=False):
"""
Calcula la cinemática inversa de un robot utilizando tres métodos:
- Levenberg-Marquardt
- Gauss-Newton
- Newton-Raphson
Args:
robot: Robot de la librería Robotics Toolbox
Td: Matriz de transformación deseada (SE3)
q0: Configuración inicial de los ángulos articulares
ilimit: Límites de iteraciones (opcional, depende del método)
mask: Máscara de restricciones (opcional, depende del método)
save_path: Ruta donde se guardarán las imágenes de los resultados
name: Nombre para guardar los archivos de imagen
status_block: Booleano para bloquear la visualización del gráfico
Returns:
dict: Diccionario con los resultados de los tres métodos
"""
print("Matriz de transformación (Inversa):")
print(Td)
# Método 1: Levenberg-Marquardt (Numérico)
sol_LM = robot.ikine_LM(Td, q0=q0, ilimit=ilimit, slimit=ilimit, mask=mask, )
print("Levenberg-Marquardt (ikine_LM):", sol_LM)
if sol_LM.success:
print("IK LM (Grados): ", np.rad2deg(sol_LM.q))
print("FK con NR:\n", robot.fkine(sol_LM.q))
robot.plot(sol_LM.q, block=status_block, jointaxes=True, eeframe=True, jointlabels=True)
plt.savefig(f"{save_path}/IK_LM_{name}.png", dpi=600, bbox_inches='tight', pad_inches=0.1)
else:
print("IK LM: No se encontró solución")
# Método 2: Gauss-Newton (Numérico)
sol_GN = robot.ikine_GN(Td, q0=q0, ilimit=ilimit, slimit=ilimit, mask=mask)
print("Gauss-Newton (ikine_GN):", sol_GN)
if sol_LM.success:
print("IK LM (Grados): ", np.rad2deg(sol_GN.q))
print("FK con GN:\n", robot.fkine(sol_GN.q))
robot.plot(sol_GN.q, block=status_block, jointaxes=True, eeframe=True, jointlabels=True)
plt.savefig(f"{save_path}/IK_GN_{name}.png", dpi=600, bbox_inches='tight', pad_inches=0.1)
else:
print("IK LM: No se encontró solución")
# Método 3: Newton-Raphson (Jacobiano)
sol_NR = robot.ikine_NR(Td, q0=q0, ilimit=ilimit, slimit=ilimit, mask=mask)
print("Newton-Raphson (ikine_NR):", sol_NR)
if sol_LM.success:
print("IK LM (Grados): ", np.rad2deg(sol_NR.q))
print("FK con LM:\n", robot.fkine(sol_NR.q))
robot.plot(sol_NR.q, block=status_block, jointaxes=True, eeframe=True, jointlabels=True)
plt.savefig(f"{save_path}/IK_NR_{name}.png", dpi=600, bbox_inches='tight', pad_inches=0.1)
else:
print("IK LM: No se encontró solución")
# Verificar cual es la mejor solución
# # Filtrar la de menores pasos
print("\nMenores iteraciones:")
if sol_LM.success and sol_LM.iterations < sol_GN.iterations and sol_LM.iterations < sol_NR.iterations:
print("Levenberg-Marquardt", sol_LM.iterations)
elif sol_GN.success and sol_GN.iterations < sol_LM.iterations and sol_GN.iterations < sol_NR.iterations:
print("Gauss-Newton", sol_GN.iterations)
elif sol_NR.success:
print("Newton-Raphson", sol_NR.iterations)
else:
print("No se encontró una solución válida")
# Verificar menores errores
print("\nMenor error:")
if sol_LM.success and sol_LM.residual < sol_GN.residual and sol_LM.residual < sol_NR.residual:
print("Levenberg-Marquardt", sol_LM.residual)
elif sol_GN.success and sol_GN.residual < sol_LM.residual and sol_GN.residual < sol_NR.residual:
print("Gauss-Newton", sol_GN.residual)
elif sol_NR.success:
print("Newton-Raphson", sol_NR.residual)
else:
print("No se encontró una solución válida")
# Resumen de success
print("\nResumen de success:")
print("Levenberg-Marquardt:", sol_LM.success)
print("Gauss-Newton:", sol_GN.success)
print("Newton-Raphson:", sol_NR.success)
return {
"Levenberg-Marquardt": sol_LM,
"Gauss-Newton": sol_GN,
"Newton-Raphson": sol_NR
}
def forward_kinematics(robot, q0, save_path, name="FK_Solution", status_block=False):
"""Calcula la cinemática directa con Denavit-Hartenberg de un robot"""
T = robot.fkine(q0) # Forward kinematics
print("Matriz de transformación (Directa):")
print(T)
try:
robot.plot(q0, block=status_block, jointaxes=True, eeframe=True, jointlabels=True)
plt.savefig(f"{save_path}/FK_{name}.png", dpi=600, bbox_inches='tight', pad_inches=0.1)
except Exception as e:
print("Error al graficar la cinemática directa:", e)
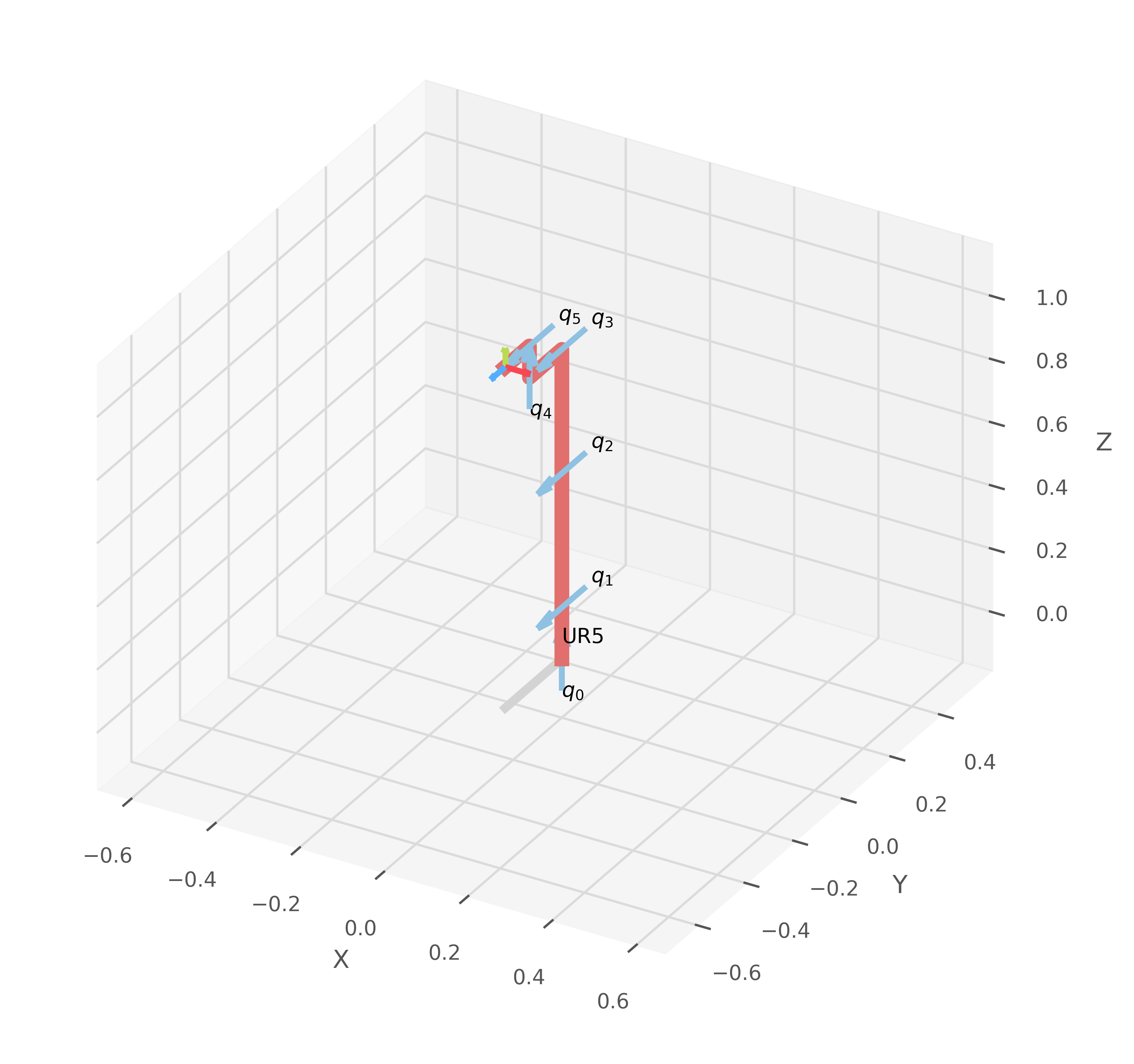
# Robot UR5 --------------------------------------------------------------
name = "UR5"
# Definir los parámetros de Denavit-Hartenberg
a1 = 0.1625
a2 = 0.425
a3 = 0.3922
a4 = 0.1333
a5 = 0.0997
a6 = 0.0996
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a1, offset=0 , qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=-a2, d=0, offset=-np.pi/2, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=-a3, d=0, offset=0, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a4, offset=-np.pi/2, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a5, offset=0, qlim=[-np.pi, np.pi]),
rtb.RevoluteDH( alpha=0, a=0, d=a6, offset=np.pi, qlim=[-2*np.pi, 2*np.pi])
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [0, 0, 0, 0, 0, 0]
d_values = [0, 0, 0, 0, 0, 0] # Example: [X, Y, Z] displacements in meters
q_values = [t_values[0], t_values[1], t_values[2], t_values[3], t_values[4], t_values[5]]
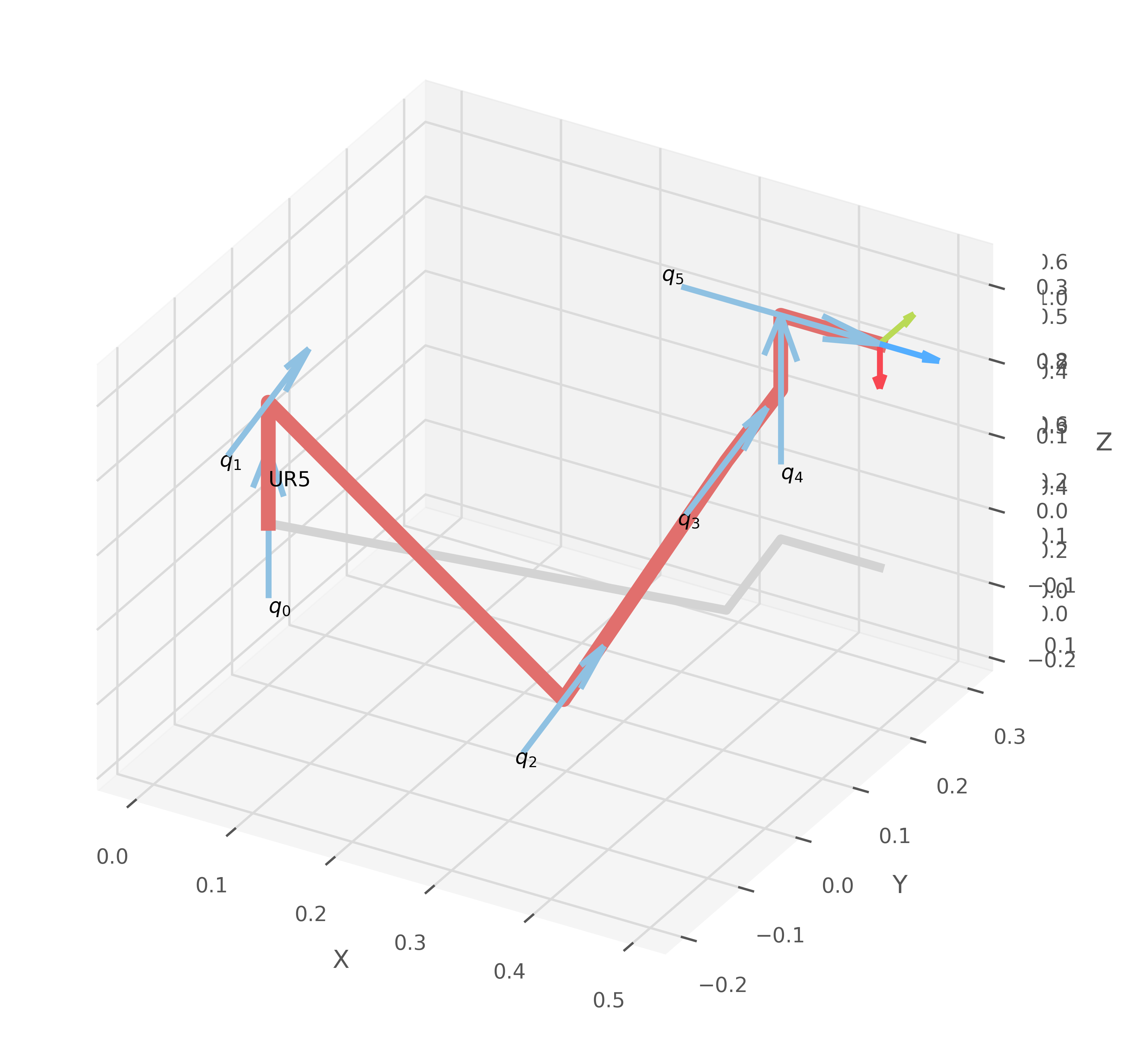
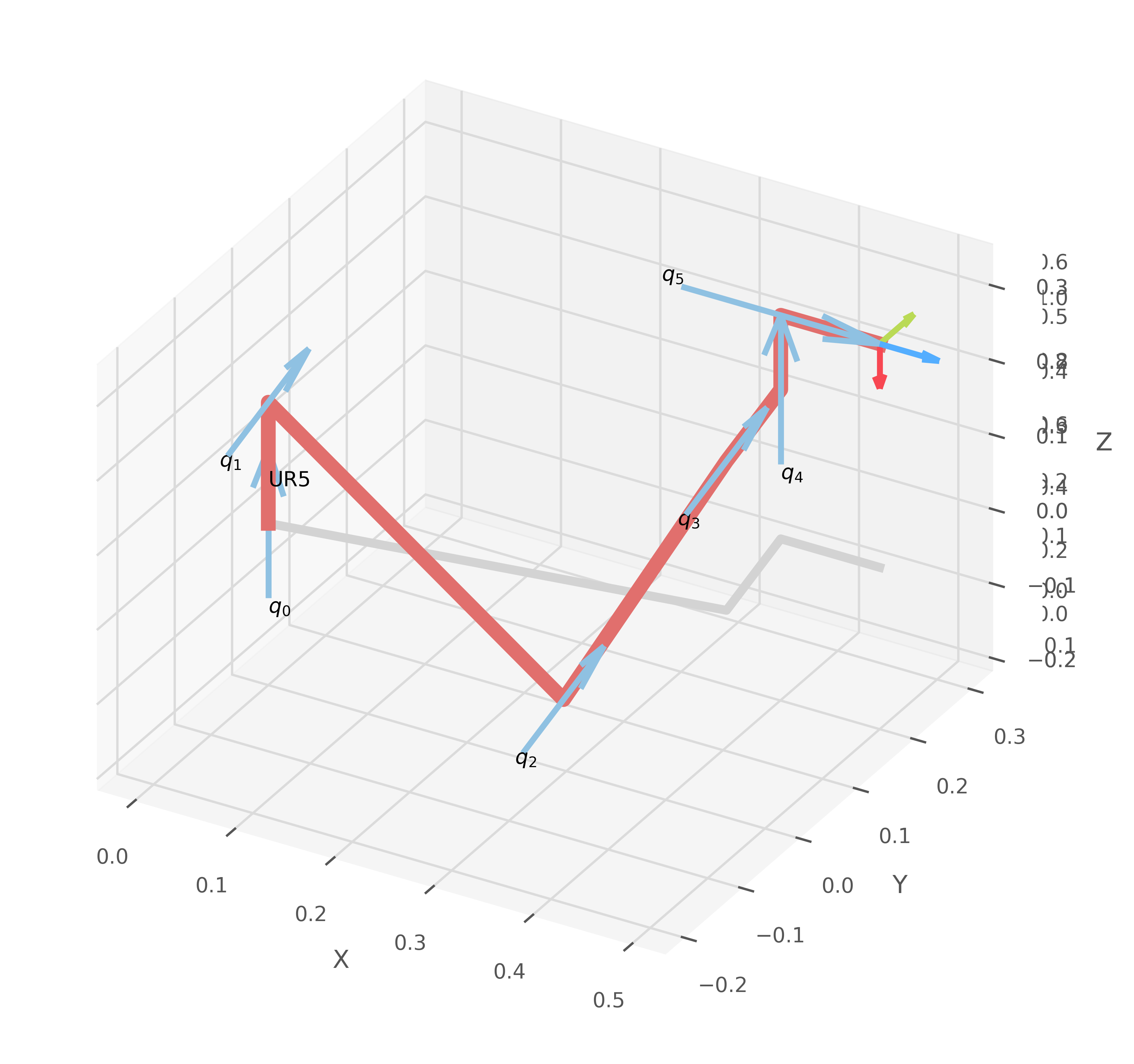
forward_kinematics(robot, q_values, save_path, name=name)
results = inverse_kinematics(robot,
SE3(0.5, 0.2, 0.3) * SE3.RPY([0, np.pi/2, 0], order="xyz"),
q0=[np.pi/2, np.pi/2, np.pi/2, np.pi/2, np.pi/2, np.pi/2],
ilimit=100,
mask=[1, 1, 1, 1, 1, 1],
save_path=save_path, name=name, status_block=False)
# Robot 1 --------------------------------------------------------------
name = "1_Planar"
# Define the planar robot with 1 revolute joint and 1 prismatic joint
a1 = 0.1 # Desplazamiento para la articulación prismática
a2 = 0.05 # Longitud del eslabón para la articulación revoluta
a3 = 0.1 # Desplazamiento adicional para la articulación prismática
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=np.pi/2, a=a2, d=0, offset=np.pi/2),
rtb.PrismaticDH( qlim=[0, 0.2], offset=a1 + a3) # Límite de la articulación prismática
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each prismatic joint
t_values = [np.radians(45)]
d_values = [0.1] # Example: [X, Y, Z] displacements in meters
q_values = [t_values[0], d_values[0]]
forward_kinematics(robot, q_values, save_path, name=name, status_block=False)
resutls = inverse_kinematics(robot,
Td = np.array([
[-0.707, 0, 0.707, 0.176],
[0.707, 0, 0.707, 0.245],
[0, 1, 0, 0],
[0, 0, 0, 1]
]),
q0=[0, 0],
ilimit=1000,
mask=[1, 1, 0, 1, 1, 0],
save_path=save_path, name=name, status_block=False)
# Robot 2 --------------------------------------------------------------
name = "2_Cartesiano"
a1 = 0.1 # Desplazamiento para la articulación prismática
a2 = 0.1 # Desplazamiento para la articulación prismática
a3 = 0.1 # Desplazamiento para la articulación prismática
# Define the Cartesian robot with 3 prismatic joints
robot = rtb.DHRobot(
[
rtb.PrismaticDH(offset=a1, alpha=-np.pi/2, a=0, theta=np.pi/2, qlim=[0, 0.2]),
rtb.PrismaticDH(offset=a2, alpha=np.pi/2, a=0, theta=-np.pi/2, qlim=[0, 0.2]),
rtb.PrismaticDH(offset=a3, alpha=0, a=0, theta=0, qlim=[0, 0.2])
],
base = SE3(0, 0, 0), # shift the entire robot 0.5m along Z
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each prismatic joint
t_values = [0]
d_values = [0.1, 0.1, 0.1] # Example: [X, Y, Z] displacements in meters
q_values = [d_values[0], d_values[1], d_values[2]]
forward_kinematics(robot, q_values, save_path, name=name, status_block=False)
results = inverse_kinematics(robot,
Td = np.array([
[1, 0, 0, 0.1],
[0, 1, 0, 0.1],
[0, 0, 1, 0.1],
[0, 0, 0, 1]
]),
q0=[.98, .98, .98],
ilimit=1000,
mask=[1, 1, 1, 0, 0, 0],
save_path=save_path, name=name, status_block=False)
# Robot 3 --------------------------------------------------------------
name = "3_Articulado"
a1 = 0.1
a2 = 0.1
a3 = 0.1
a4 = 0.1
a5 = 0.1
a6 = 0.1
# longitud del eslabón para la articulación revoluta
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a1, offset=0),
rtb.RevoluteDH( alpha=0, a=a2, d=0, offset=-np.pi/2),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a3+a4, offset=np.pi/2),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=0, a=0, d=a5+a6, offset=0)
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi, 0, np.pi, 0, 0, 0]
d_values = [0, 0, 0, 0, 0, 0] # Example: [X, Y, Z] displacements in meters
q_values = [t_values[0], t_values[1], t_values[2], t_values[3], t_values[4], t_values[5]]
forward_kinematics(robot, q_values, save_path, name=name, status_block=False)
results = inverse_kinematics(robot,
Td = np.array([
[0, 0, 1, 0.4],
[1, 0, 0, 0],
[0, 1, 0, 0.2],
[0, 0, 0, 1]
]),
q0=[np.pi, 0, np.pi, 0, 0, 0],
ilimit=1000,
mask=[1, 1, 1, 0, 0, 0],
save_path=save_path, name=name, status_block=False)
# Robot 4 --------------------------------------------------------------
name = "4_Articulado"
a1 = 0.2
a2 = 0.1
a3 = 0.1
a4 = 0.1
a5 = 0.1
a6 = 0.1
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a1, offset=0),
rtb.RevoluteDH( alpha=-np.pi/2, a=a2, d=0, offset=0),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=a3+a4, offset=0),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=0, a=0, d=a5+a6, offset=0)
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi, 0, np.pi, 0, 0, 0]
d_values = [0, 0, 0, 0, 0, 0] # Example: [X, Y, Z] displacements in meters
q_values = [t_values[0], t_values[1], t_values[2], t_values[3], t_values[4], t_values[5]]
forward_kinematics(robot, q_values, save_path, name=name, status_block=False)
results = inverse_kinematics(robot,
Td = np.array([
[1, 0, 0, -0.1],
[0, 0, -1,-0.4],
[0, 1, 0, 0.2],
[0, 0, 0, 1]
]),
q0=[np.pi, 0, np.pi/2, 0, 0, 0],
ilimit=1000,
mask=[1, 1, 1, 0, 0, 0],
save_path=save_path, name=name, status_block=False)
# Robot 5 --------------------------------------------------------------
name = "5_Articulado"
a1 = 0.1
a2 = 0.1
a3 = 0.1
a4 = 0.1
a5 = 0.1
a6 = 0.1
# Define the articulated robot with 6 revolute joints
robot = rtb.DHRobot(
[
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a1, offset=0),
rtb.RevoluteDH( alpha=0, a=a2, d=0, offset=-np.pi/2),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=-np.pi/2, a=0, d=a3+a4, offset=0),
rtb.RevoluteDH( alpha=np.pi/2, a=0, d=0, offset=0),
rtb.RevoluteDH( alpha=0, a=0, d=a5+a6, offset=0)
],
name=name
)
print("Detalles del Robot: ", name)
print(robot)
# Define the displacement values for each revolute joint
t_values = [np.pi, 0, np.pi, 0, 0, 0]
d_values = [0, 0, 0, 0, 0, 0] # Example: [X, Y, Z] displacements in meters
q_values = [t_values[0], t_values[1], t_values[2], t_values[3], t_values[4], t_values[5]]
forward_kinematics(robot, q_values, save_path, name=name, status_block=False)
results = inverse_kinematics(robot,
Td = np.array([
[0, 0, -1, -0.4],
[0, -1, 0, 0],
[-1, 0, 0, 0.2],
[0, 0, 0, 1]
]),
q0=[np.pi, 0, np.pi/2, 0, 0, 0],
ilimit=1000,
mask=[1, 1, 1, 0, 0, 0],
save_path=save_path, name=name, status_block=False)

DHRobot: UR5, 6 joints (RRRRRR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| q1 | 0.1625 | 0 | 90.0° | -180.0° | 180.0° |
| q2 - 90° | 0 | -0.425 | 0.0° | -180.0° | 180.0° |
| q3 | 0 | -0.3922 | 0.0° | -180.0° | 180.0° |
| q4 - 90° | 0.1333 | 0 | 90.0° | -180.0° | 180.0° |
| q5 | 0.0997 | 0 | -90.0° | -180.0° | 180.0° |
| q6 + 180° | 0.0996 | 0 | 0.0° | -360.0° | 360.0° |
Matriz de transformación (Directa):
1 0 0 0
0 0 -1 -0.2329
0 1 0 1.079
0 0 0 1
Matriz de transformación (Inversa):
0 0 1 0.5
0 1 0 0.2
-1 0 0 0.3
0 0 0 1
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[-2.981, 0.187, 1.862, 1.093, 1.732, 1.571], success=True, iterations=8, searches=1, residual=4.81e-08
IK LM (Grados):
[-170.785 10.714 106.67 62.616 99.215 90.000]
FK con NR:
-4.757e-11 2.2e-11 1 0.5
7.325e-10 1 -2.2e-11 0.2
-1 7.325e-10 -4.757e-11 0.3
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[-2.981, 2.437, -2.039, -0.3978, -1.732, -1.571], success=True, iterations=11, searches=1, residual=3.89e-11
IK LM (Grados):
[-170.785 139.624 -116.83 -22.794 -99.215 -90.000]
FK con GN:
-9.492e-08 5.395e-08 1 0.5
-1.263e-07 1 -5.395e-08 0.2
-1 -1.263e-07 -9.492e-08 0.3
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[-2.981, 2.437, -2.039, -0.3978, -1.732, -1.571], success=True, iterations=11, searches=1, residual=3.89e-11
IK LM (Grados):
[-170.785 139.624 -116.83 -22.794 -99.215 -90.000]
FK con LM:
-9.492e-08 5.395e-08 1 0.5
-1.263e-07 1 -5.395e-08 0.2
-1 -1.263e-07 -9.492e-08 0.3
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (8)
Menor error: Newton-Raphson (3.89e-11)
Resumen de success:


Detalles del Robot: 1_Planar
DHRobot: 1_Planar, 2 joints (RP), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| q1 + 90° | 0 | 0.05 | 90.0° | -180.0° | 180.0° |
| 0.0° | q2 + 0.2 | 0 | 0.0° | 0.0 | 0.2 |
Matriz de transformación (Directa):
-0.7071 0 0.7071 0.1768
0.7071 0 0.7071 0.2475
0 1 0 0
0 0 0 1
Matriz de transformación (Inversa):
[[-0.707 0. 0.707 0.176]
[ 0.707 0. 0.707 0.245]
[ 0. 1. 0. 0. ]
[ 0. 0. 0. 1. ]]
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[0.7813, 0.09749], success=True, iterations=4, searches=1, residual=1.95e-08
IK LM (Grados):
[44.76711445 5.58583301]
FK con NR:
-0.7042 0 0.71 0.176
0.71 0 0.7042 0.245
0 1 0 0
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[1.416, 0.1467], success=False, reason=iteration and search limit reached, 1000 numpy.LinAlgError encountered, iterations=1000, searches=1000, residual=0
IK LM (Grados):
[81.10729219 8.40261884]
FK con GN:
-0.988 0 0.1546 0.004188
0.1546 0 0.988 0.3502
0 1 0 0
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[0.9705, 0.1463], success=False, reason=iteration and search limit reached, 1000 numpy.LinAlgError encountered, iterations=1000, searches=1000, residual=0
IK LM (Grados):
[55.6051253 8.38360618]
FK con LM:
-0.8252 0 0.5649 0.1544
0.5649 0 0.8252 0.314
0 1 0 0
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (4)
Menor error: No se encontró una solución válida
Resumen de success:

Detalles del Robot: 2_Cartesiano
DHRobot: 2_Cartesiano, 3 joints (PPP), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ | q⁻ | q⁺ |
|---|---|---|---|---|---|
| 90.0° | q1 + 0.1 | 0 | -90.0° | 0.0 | 0.2 |
| -90.0° | q2 + 0.1 | 0 | 90.0° | 0.0 | 0.2 |
| 0.0° | q3 + 0.1 | 0 | 0.0° | 0.0 | 0.2 |
Matriz de transformación (Directa):
0 -1 0 -0.2
0 0 -1 -0.2
1 0 0 0.2
0 0 0 1
Matriz de transformación (Inversa):
[[1. 0. 0. 0.1]
[0. 1. 0. 0.1]
[0. 0. 1. 0.1]
[0. 0. 0. 1. ]]
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[0, -0.2, -0.2], success=True, iterations=5, searches=1, residual=2.31e-08
IK LM (Grados):
[ 1.44193627e-10 -1.14591559e+01 -1.14591559e+01]
FK con NR:
0 -1 0 0.1
0 0 -1 0.1
1 0 0 0.1
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[0.1217, 0.04879, 0.0449], success=False, reason=iteration and search limit reached, 1000 numpy.LinAlgError encountered, iterations=1000, searches=1000, residual=0
IK LM (Grados):
[6.97439252 2.79525679 2.57247966]
FK con GN:
0 -1 0 -0.1488
0 0 -1 -0.1449
1 0 0 0.2217
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[0.03493, 0.1481, 0.05422], success=False, reason=iteration and search limit reached, 1000 numpy.LinAlgError encountered, iterations=1000, searches=1000, residual=0
IK LM (Grados):
[2.00160656 8.48666888 3.10658856]
FK con LM:
0 -1 0 -0.2481
0 0 -1 -0.1542
1 0 0 0.1349
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (5)
Menor error: No se encontró una solución válida
Resumen de success:



Detalles del Robot: 3_Articulado
DHRobot: 3_Articulado, 6 joints (RRRRRR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ |
|---|---|---|---|
| q1 | 0.1 | 0 | -90.0° |
| q2 - 90° | 0 | 0.1 | 0.0° |
| q3 | 0 | 0 | -90.0° |
| q4 + 90° | 0.2 | 0 | 90.0° |
| q5 | 0 | 0 | -90.0° |
| q6 | 0.2 | 0 | 0.0° |
Matriz de transformación (Directa):
0 0 1 0.4
1 0 0 0
0 1 0 0.2
0 0 0 1
Matriz de transformación (Inversa):
[[0. 0. 1. 0.4]
[1. 0. 0. 0. ]
[0. 1. 0. 0.2]
[0. 0. 0. 1. ]]
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[0.4142, 1.583, -2.296, 0.5448, -1.226, 1.117], success=True, iterations=5, searches=2, residual=2.64e-07
IK LM (Grados):
[23.7345 90.6891 -131.5433 31.2162 -70.2666 64.0179]
FK con NR:
0.08414 0.5202 0.8499 0.4
0.4077 0.7603 -0.5057 3.89e-07
-0.9092 0.3891 -0.1481 0.2
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[3.142, 0, 3.142, 1.323, -4.114e-05, -1.323], success=True, iterations=111, searches=2, residual=8.61e-07
IK LM (Grados):
[179.9998 0.0000249 179.9976 75.8189 -0.002357 -75.8189]
FK con GN:
-6.279e-06 1.318e-06 1 0.4
1 4.286e-09 6.279e-06 4.958e-07
-4.277e-09 1 -1.318e-06 0.2
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[0, 0, 0, -2.62, 0, -0.5211], success=True, iterations=31, searches=2, residual=4.95e-09
IK LM (Grados):
[0.000000 -0.0000081 0.0000081 -150.1433 0.000000 -29.8567]
FK con LM:
8.497e-11 2.956e-11 1 0.4
1 -2.335e-08 -8.497e-11 -5.64e-12
2.335e-08 1 -2.956e-11 0.2
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (5)
Menor error: Newton-Raphson (4.95e-09)
Resumen de success:


Detalles del Robot: 4_Articulado
DHRobot: 4_Articulado, 6 joints (RRRRRR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ |
|---|---|---|---|
| q1 | 0.2 | 0 | -90.0° |
| q2 | 0 | 0.1 | -90.0° |
| q3 | 0 | 0 | -90.0° |
| q4 | 0.2 | 0 | 90.0° |
| q5 | 0 | 0 | -90.0° |
| q6 | 0.2 | 0 | 0.0° |
Matriz de transformación (Directa):
1 0 0 -0.1
0 0 -1 -0.4
0 1 0 0.2
0 0 0 1
Matriz de transformación (Inversa):
[[ 1. 0. 0. -0.1]
[ 0. 0. -1. -0.4]
[ 0. 1. 0. 0.2]
[ 0. 0. 0. 1. ]]
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[-3.108, 0, 3.046, 0, 0.2584, 0], success=True, iterations=6, searches=1, residual=1.27e-09
IK LM (Grados):
[-178.09 0.00 174.52 0.00 14.80 0.00]
FK con NR:
0.9916 0 -0.129 -0.1
-0.129 0 -0.9916 -0.4
0 1 0 0.2
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[3.142, 5.011e-05, 3.142, -0.8475, -1.449e-05, 0.8475], success=True, iterations=20, searches=2, residual=9.73e-07
IK LM (Grados):
[179.99 0.00287 179.99 -48.56 -0.00083 48.55]
FK con GN:
1 -5.057e-06 1.541e-05 -0.1
1.541e-05 -1.086e-05 -1 -0.4
5.057e-06 1 -1.086e-05 0.2
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[3.142, 0, 3.142, 1.607, 0, -1.607], success=True, iterations=134, searches=2, residual=1.37e-10
IK LM (Grados):
[180.00 -0.00000075 180.00 92.08 -0.00000038 -92.08]
FK con LM:
1 2.201e-10 2.596e-09 -0.1
2.596e-09 6.618e-09 -1 -0.4
-2.201e-10 1 6.618e-09 0.2
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (6)
Menor error: Newton-Raphson (1.37e-10)
Resumen de success:
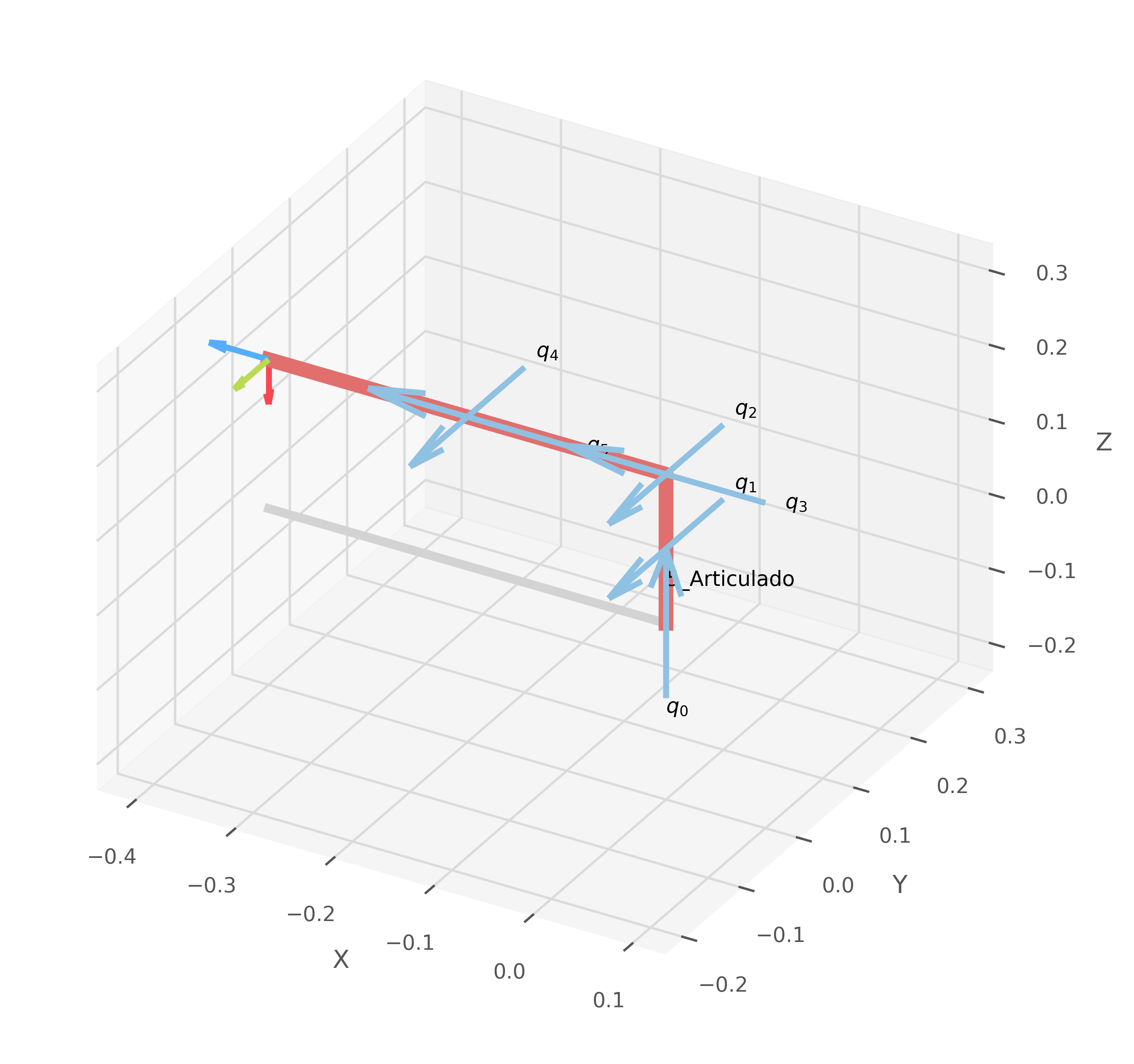

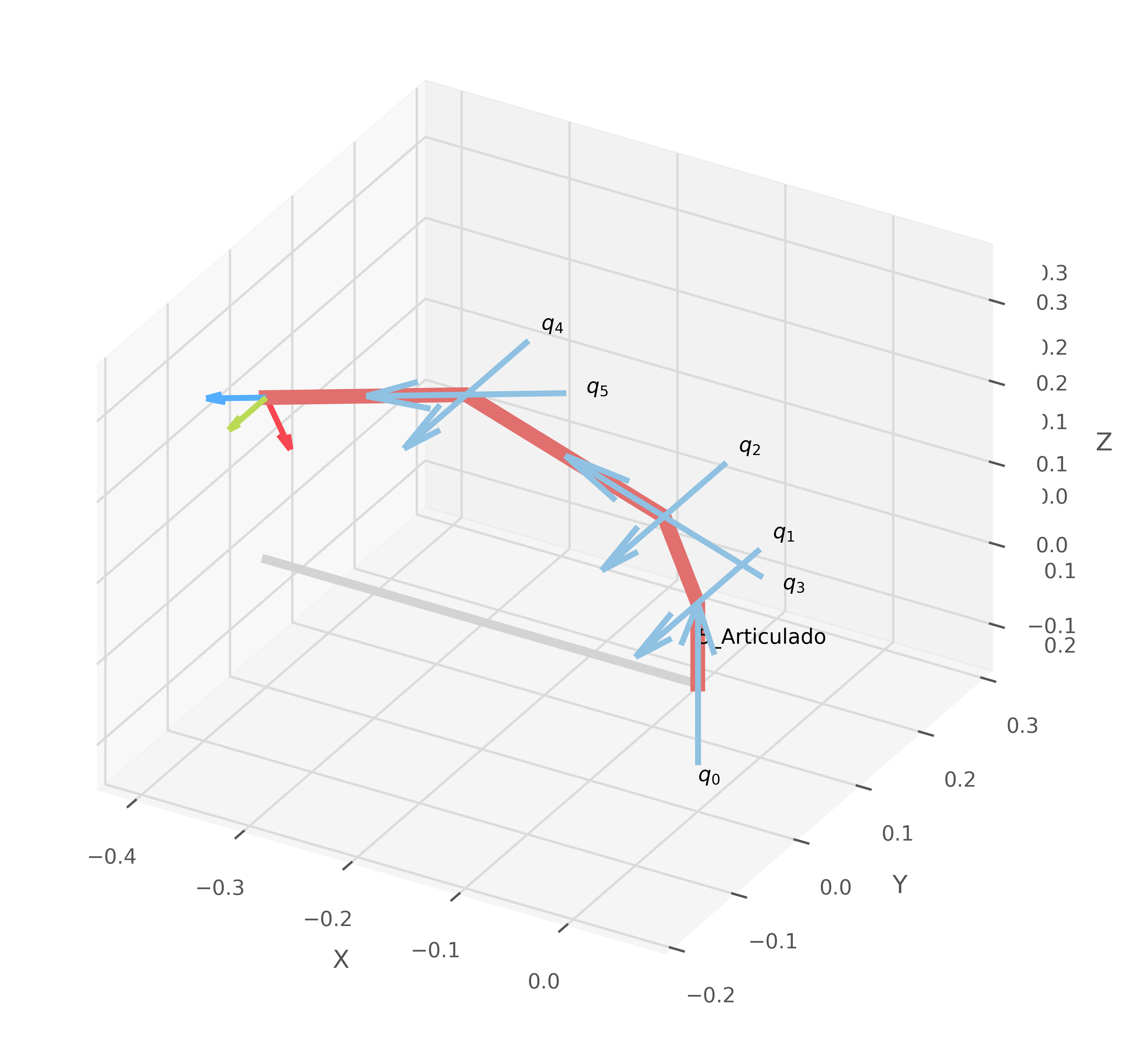

Detalles del Robot: 5_Articulado
DHRobot: 5_Articulado, 6 joints (RRRRRR), dynamics, standard DH parameters
| θⱼ | dⱼ | aⱼ | ⍺ⱼ |
|---|---|---|---|
| q1 | 0.1 | 0 | -90.0° |
| q2 - 90° | 0 | 0.1 | 0.0° |
| q3 | 0 | 0 | 90.0° |
| q4 | 0.2 | 0 | -90.0° |
| q5 | 0 | 0 | 90.0° |
| q6 | 0.2 | 0 | 0.0° |
Matriz de transformación (Directa):
0 0 -1 -0.4
0 -1 0 0
-1 0 0 0.2
0 0 0 1
Matriz de transformación (Inversa):
[[ 0. 0. -1. -0.4]
[ 0. -1. 0. 0. ]
[-1. 0. 0. 0.2]
[ 0. 0. 0. 1. ]]
Levenberg-Marquardt (ikine_LM):
IKSolution: q=[-3.142, 0.3181, 2.412, 0, 0.7957, 0], success=True, iterations=6, searches=1, residual=2.97e-11
IK LM (Grados):
[-180.00 18.23 138.20 0.00 45.59 0.00]
FK con NR:
0.3749 0 -0.9271 -0.4
0 -1 0 0
-0.9271 0 -0.3749 0.2
0 0 0 1
Gauss-Newton (ikine_GN):
IKSolution: q=[0, -2.214, -3.142, 3.142, 0.9273, 0], success=True, iterations=56, searches=2, residual=2.42e-10
IK LM (Grados):
[-0.00 -126.87 -180.00 180.00 53.13 0.00]
FK con GN:
-2.421e-09 -1.208e-09 -1 -0.4
-4.467e-10 -1 1.208e-09 4.4e-10
-1 4.467e-10 2.421e-09 0.2
0 0 0 1
Newton-Raphson (ikine_NR):
IKSolution: q=[0, 1.318e-06, -1.848e-05, -0.1227, 1.7e-05, -3.019], success=True, iterations=10, searches=2, residual=3.78e-07
IK LM (Grados):
[-0.00 0.00 -0.11 -7.03 0.00 -172.97]
FK con LM:
2.93e-07 1.971e-06 -1 -0.4
-9.144e-08 -1 -1.971e-06 -3.724e-07
-1 9.144e-08 -2.93e-07 0.2
0 0 0 1
Menores iteraciones: Levenberg-Marquardt (6)
Menor error: Levenberg-Marquardt (2.97e-11)
Resumen de success: