Introducción
Se utiliza un análisis geométrico de los robots para su cinemática inversa.
Descargar teoría PDF
Se utiliza un análisis geométrico de los robots para su cinemática inversa.
Descargar teoría PDF
import sympy as sp
import numpy as np
# Robot esferico --------------------------------------------------------------
name = "Robot Esferico"
th1, th2 = sp.symbols('th1 th2')
a1, a2, a3, a4, a5, h, d1 = sp.symbols('a1 a2 a3 a4 a5 h d1')
x, y, z = sp.symbols('x y z')
a4 = z-a1
a5 = sp.sqrt(x**2 + y**2)
h=sp.sqrt(a5**2 + a4**2)
d1 = h -a2 -a3
th1 = sp.atan(y/x)
th2 = sp.atan(a4/a5)
# Mostrar los resultados
print(f"\n--- Inverse by Geometry {name} ---")
print("th1:", sp.deg(th1))
print("th2:", sp.deg(th2))
print("d1:", d1)
# Robot articulado -----------------------------------------------------------
name = "Robot Articulado"
th1, th2, th3 = sp.symbols('th1 th2 th3')
a1, a2, a3, n1, n2, n3 = sp.symbols('a1 a2 a3 n1 n2 n3')
x, y, z = sp.symbols('x y z')
n1 = z-a1
n2 = sp.sqrt(x**2 + y**2)
n3 = sp.sqrt(n1**2 + n2**2)
alpha1 = sp.atan(n1/n2)
alpha2 = sp.acos(-(a3**2 - (a2**2) - (n3**2))/(2*a2*n3))
alpha3 = sp.acos(-(n3**2 - (a2**2) - (a3**2))/(2*a2*a3))
th1 = sp.atan(y/x)
th2 = alpha1 - alpha2
th3 = sp.rad(180) - alpha3
# Mostrar los resultados
print(f"\n--- Inverse by Geometry {name} ---")
print("th1:", sp.deg(th1))
print("th2:", sp.deg(th2))
print("th3:", sp.deg(th3))
# Robot PRP V_alineado ------------------------------------------------------------------
name = "Robot PRP V_alineado"
th1 = sp.symbols('th1')
d1, d2 = sp.symbols('d1 d2')
a1, a2 = sp.symbols('a1 a2')
x, y, z = sp.symbols('x y z')
d1 = z - a1
d2 = sp.sqrt(x**2 + y**2)-a2
th1 = sp.atan(y/x)
# Mostrar los resultados
print(f"\n--- Inverse by Geometry {name} ---")
print("th1:", sp.deg(th1))
print("d1:", d1)
print("d2:", d2)
# Robot PRP V_no_alineado ------------------------------------------------------------------
name = "Robot PRP V_no_alineado"
th1 = sp.symbols('th1')
d1, d2 = sp.symbols('d1 d2')
a1, a2, a3, h, phi1, phi2 = sp.symbols('a1 a2 a3 h phi1 phi2')
x, y, z = sp.symbols('x y z')
h = sp.sqrt(x**2 + y**2)
phi1 = sp.atan(x/y)
phi2 = sp.atan(a3/h)
d1 = z - a1
d2 = (sp.atan(phi2)*a3)-a2
th1 = sp.atan(y/x)
# Mostrar los resultados
print(f"\n--- Inverse by Geometry {name} ---")
print("th1:", sp.deg(th1))
print("d1:", d1)
print("d2:", d2)
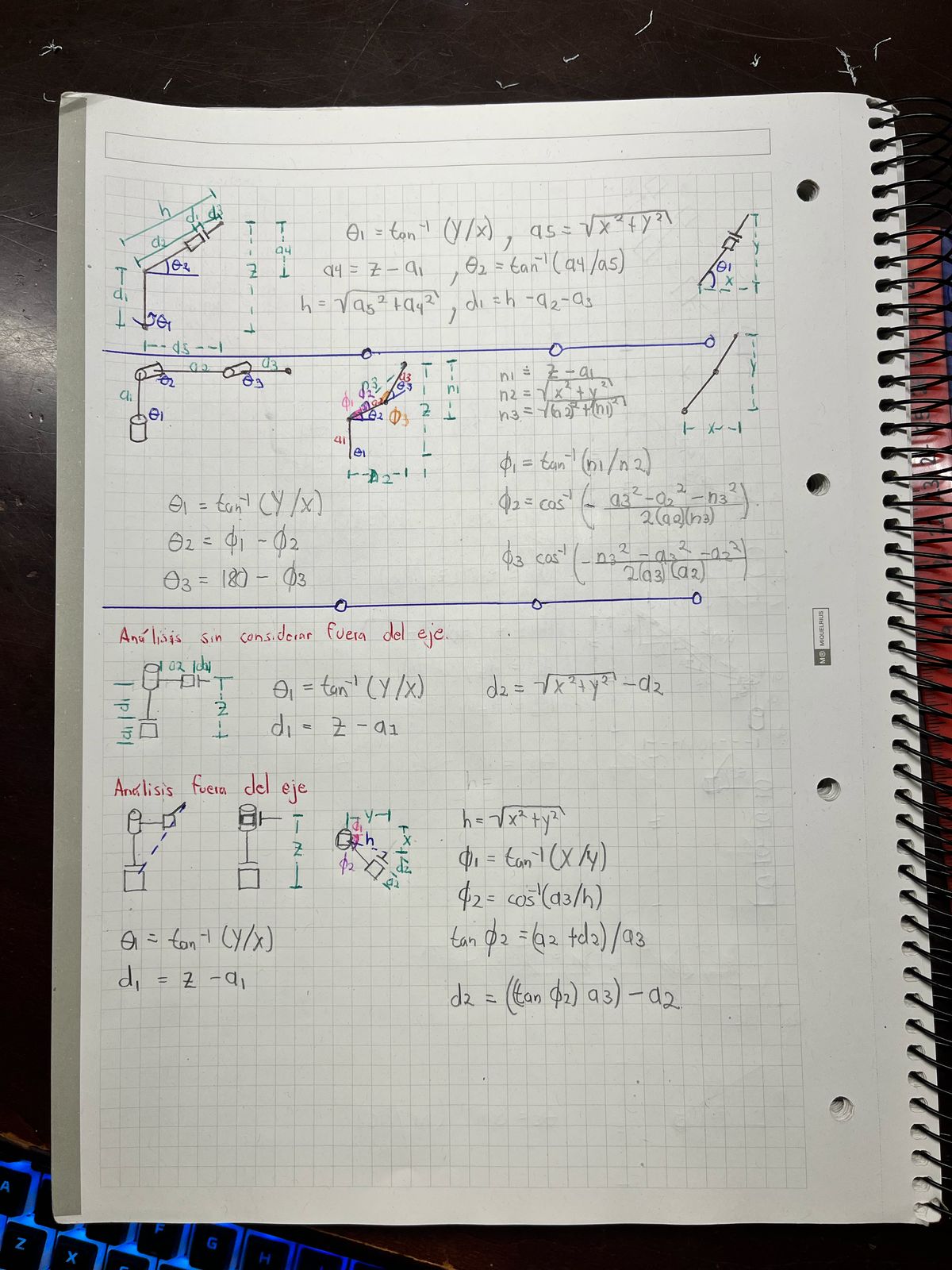
Se presentan 3 robots: Esférico, Articulado & PRP