import sympy as sp
# Función para calcular la matriz homogénea
def dh_matrix(theta, d, a, alpha):
return sp.Matrix([
[sp.cos(theta), -sp.sin(theta)*sp.cos(alpha), sp.sin(theta)*sp.sin(alpha), a*sp.cos(theta)],
[sp.sin(theta), sp.cos(theta)*sp.cos(alpha), -sp.cos(theta)*sp.sin(alpha), a*sp.sin(theta)],
[0, sp.sin(alpha), sp.cos(alpha), d],
[0, 0, 0, 1]
])
#dh_matrix(θ, d , a, α)
# Función para generar una matriz de rotación homogénea
def rotation_matrix(x_angle=0, y_angle=0, z_angle=0):
# Rotación alrededor del eje X
R_x = sp.Matrix([
[1, 0, 0, 0],
[0, sp.cos(x_angle), -sp.sin(x_angle), 0],
[0, sp.sin(x_angle), sp.cos(x_angle), 0],
[0, 0, 0, 1]
])
# Rotación alrededor del eje Y
R_y = sp.Matrix([
[sp.cos(y_angle), 0, sp.sin(y_angle), 0],
[0, 1, 0, 0],
[-sp.sin(y_angle), 0, sp.cos(y_angle), 0],
[0, 0, 0, 1]
])
# Rotación alrededor del eje Z
R_z = sp.Matrix([
[sp.cos(z_angle), -sp.sin(z_angle), 0, 0],
[sp.sin(z_angle), sp.cos(z_angle), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
# Matriz de rotación combinada
return R_x @ R_y @ R_z # Usar @ para multiplicación de matrices
def reemplazar_trigonometria(matriz, n=3):
"""
Reemplaza las funciones trigonométricas en la matriz:
sin -> S
cos -> C
y evalúa los valores numéricos con 2 decimales.
"""
matriz_reemplazada = matriz.applyfunc(lambda expr: expr.replace(sp.sin, lambda x: sp.Symbol(f'S({x})')).replace(sp.cos, lambda x: sp.Symbol(f'C({x})')))
return matriz_reemplazada.evalf(n)
n=3
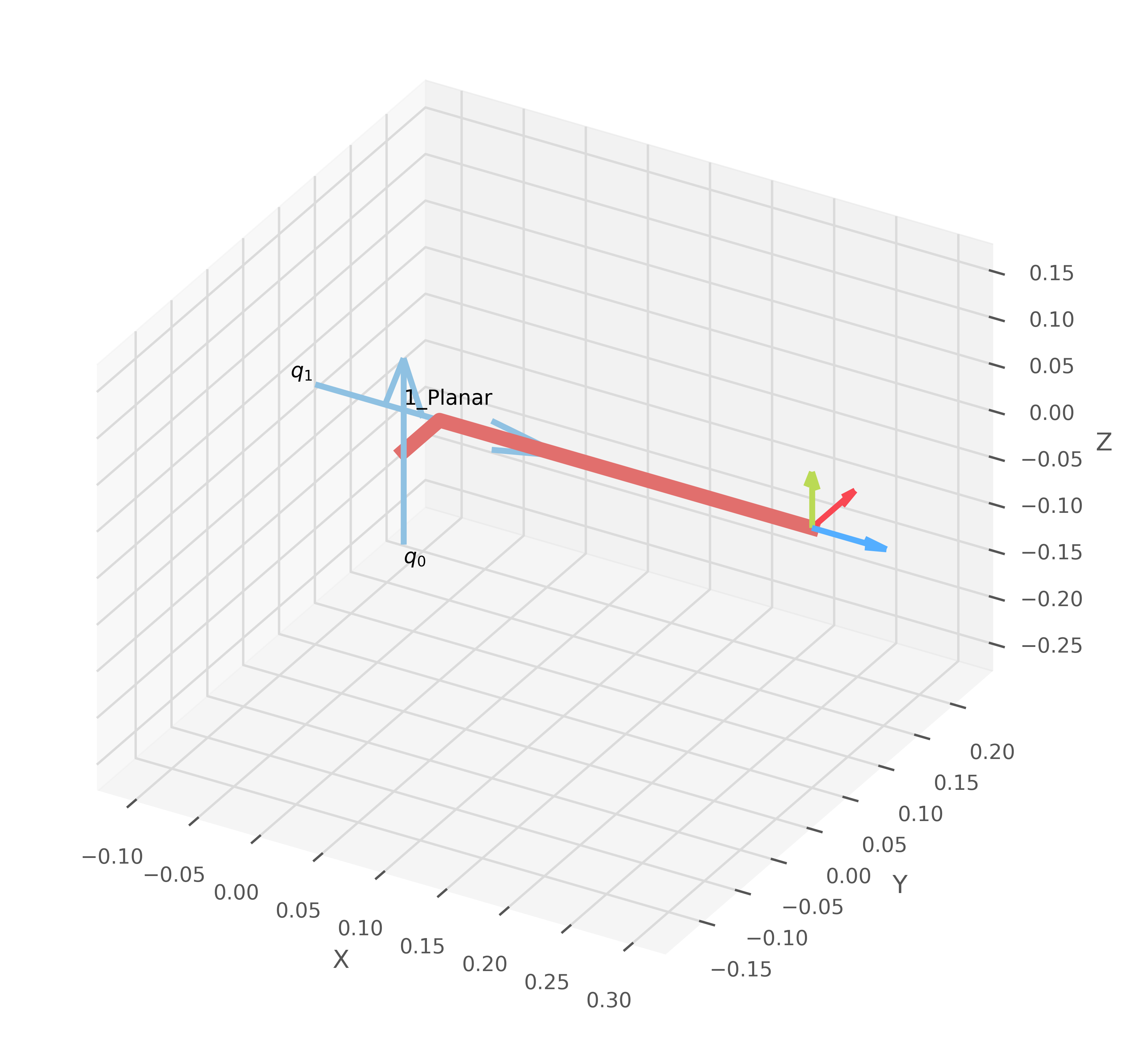
# Ejercicio 1:
print("\nEjercicio 1:")
# Definir las variables simbólicas
th1, a2, a1, a3, d1 = sp.symbols('th1 a2 a1 a3 d1')
# Primera fila de la tabla DH: [α=90, a=a2, θ=θ1, d=0]
T1 = dh_matrix(th1, 0, a2, sp.pi/2)
# Segunda fila de la tabla DH: [α=0, a=0, θ=0, d=a1 + a3 + d1]
T2 = dh_matrix(0, a1 + a3 + d1, 0, 0)
# Matriz final: Producto de las transformaciones
T = T1 @ T2
# Mostrar las matrices individuales y el producto final, redondeado a 2 decimales
print("Matriz T1:")
sp.pprint(reemplazar_trigonometria(T1)) # Redondear a 2 decimales
print("\nMatriz T2:")
sp.pprint(reemplazar_trigonometria(T2)) # Redondear a 2 decimales
print("\nMatriz homogénea total T:")
sp.pprint(reemplazar_trigonometria(T)) # Redondear a 2 decimales
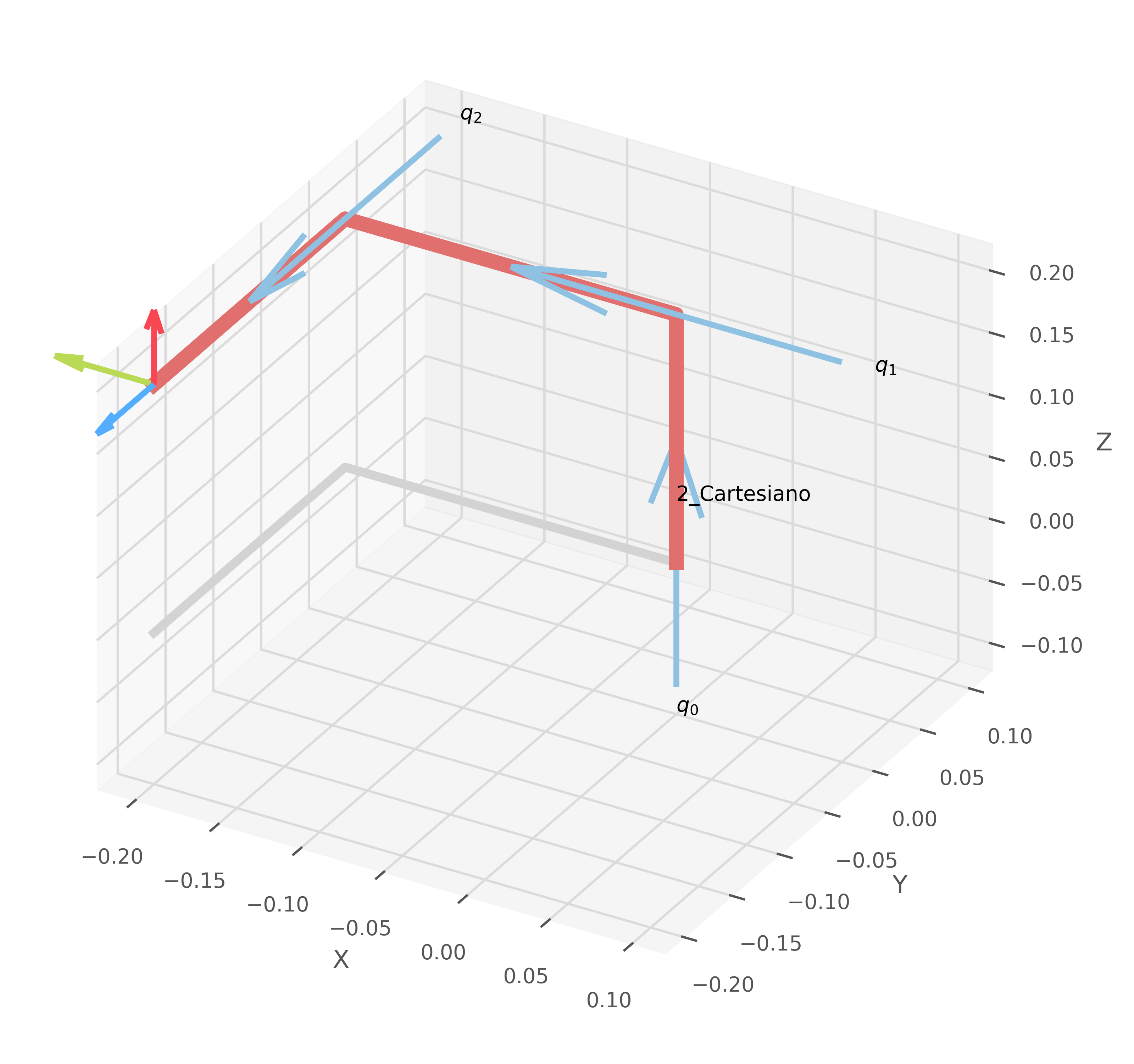
# Ejercicio 2:
print("\nEjercicio 2:")
# Definir las variables simbólicas
a2, a1, a3, d1, d2, d3 = sp.symbols('a2 a1 a3 d1 d2 d3')
# Primera fila de la tabla DH: [α=-90, a=0, θ=90, d=a1+d1]
T1 = dh_matrix(sp.pi/2, a1 + d1, 0, -sp.pi/2)
# Segunda fila de la tabla DH: [α=90, a=0, θ=-90, d=a2+d2]
T2 = dh_matrix(-sp.pi/2, a2 + d2, 0, sp.pi/2)
# Tercera fila de la tabla DH: [α=0, a=0, θ=0, d=a3+d3]
T3 = dh_matrix(0, a3 + d3, 0, 0)
# Matriz final: Producto de las transformaciones
T = T1 @ T2 @ T3
# Mostrar las matrices individuales y el producto final, redondeado a 2 decimales
print("Matriz T1:")
sp.pprint(reemplazar_trigonometria(T1)) # Redondear a 2 decimales
print("\nMatriz T2:")
sp.pprint(reemplazar_trigonometria(T2)) # Redondear a 2 decimales
print("\nMatriz T3:")
sp.pprint(reemplazar_trigonometria(T3)) # Redondear a 2 decimales
print("\nMatriz homogénea total T:")
sp.pprint(reemplazar_trigonometria(sp.simplify(T))) # Redondear a 2 decimales
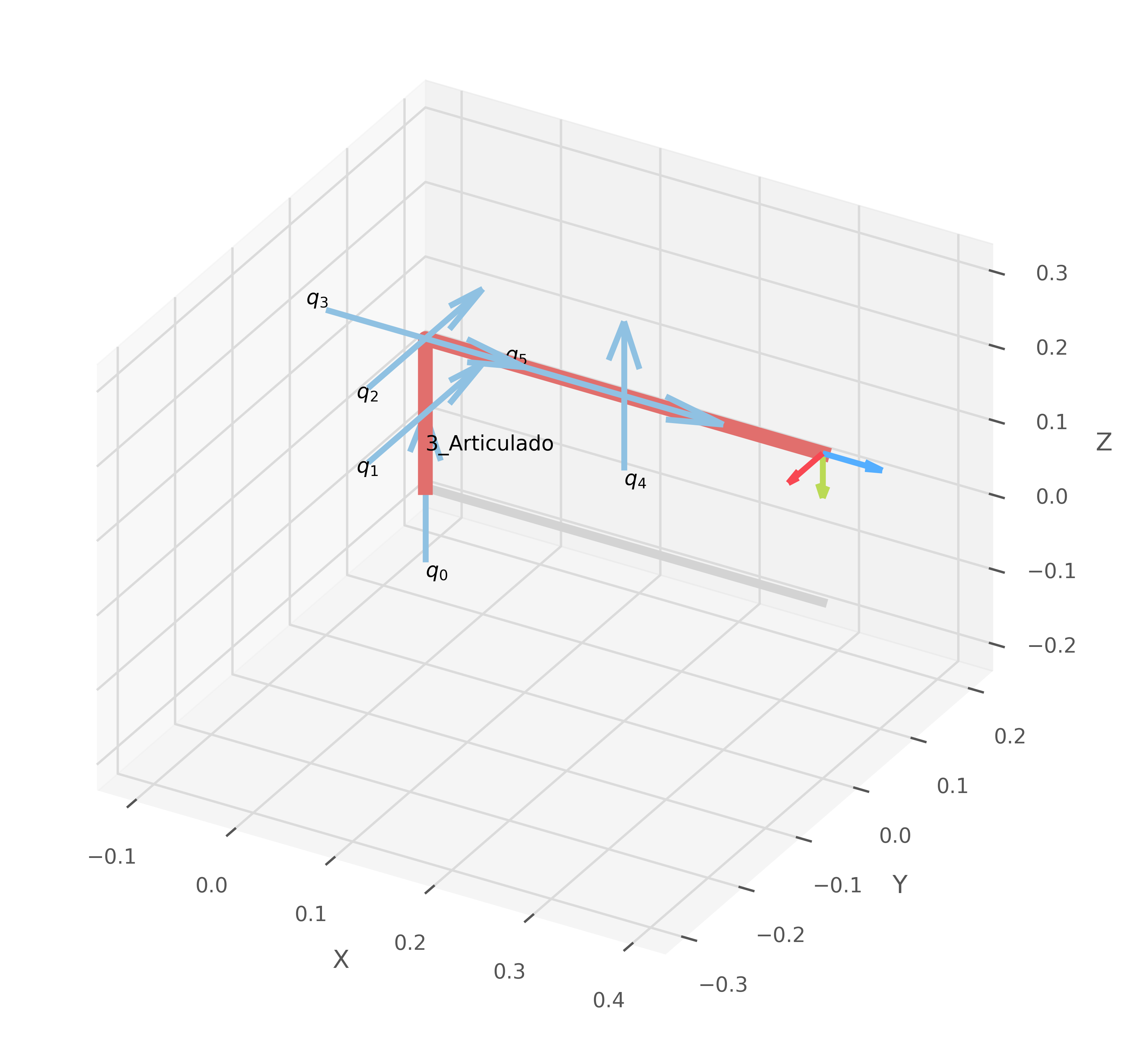
# Ejercicio 3:
print("\nEjercicio 3:")
# Definir las variables simbólicas
th1, th2, th3, th4, th5, th6, d1, d2, d3, d4, d5, d6 = sp.symbols('th1 th2 th3 th4 th5 th6 d1 d2 d3 d4 d5 d6')
# Primera fila de la tabla DH: [α=-90, a=0, θ=th1, d=d1]
T1 = dh_matrix(th1, d1, 0, -sp.pi/2)
# Segunda fila de la tabla DH: [α=0, a=d2, θ=th2, d=0]
T2 = dh_matrix(th2, 0, d2, 0)
# Tercera fila de la tabla DH: [α=0, a=d3, θ=th3, d=0]
T3 = dh_matrix(th3, 0, d3, 0)
#------------Roptura de robot por no cumplir denavit----------------
# Cuarta fila de la tabla DH: [α=-90, a=0, θ=th4, d=d4]
T4 = dh_matrix(th4, d4, 0, -sp.pi/2)
# Quinta fila de la tabla DH: [α=90, a=d5, θ=th5, d=0]
T5 = dh_matrix(th5, 0, d5, sp.pi/2)
# Sexta fila de la tabla DH: [α=0, a=0, θ=th6, d=d6]
T6 = dh_matrix(th6, d6, 0, 0)
# Matriz final: Producto de las transformaciones
T_1 = T1 * T2 * T3
T_2 = T4 * T5 * T6
# Mostrar las matrices individuales y el producto final, redondeado a 2 decimales
print("Matriz T1:")
sp.pprint(reemplazar_trigonometria(T1)) # Redondear a 2 decimales
print("\nMatriz T2:")
sp.pprint(reemplazar_trigonometria(T2)) # Redondear a 2 decimales
print("\nMatriz T3:")
sp.pprint(reemplazar_trigonometria(T3)) # Redondear a 2 decimales
print("\nMatriz T4:")
sp.pprint(reemplazar_trigonometria(T4)) # Redondear a 2 decimales
print("\nMatic T5:")
sp.pprint(reemplazar_trigonometria(T5)) # Redondear a 2 decimales
print("\nMatiz T6:")
sp.pprint(reemplazar_trigonometria(T6)) # Redondear a 2 decimales
print("\nMatriz homogénea total T1:")
sp.pprint(reemplazar_trigonometria(T_1)) # Redondear a 2 decimales
print("\nMatriz homogénea total T2:")
sp.pprint(reemplazar_trigonometria(T_2)) # Redondear a 2 decimales
# Juntar las matrices T1 y T2
x_angle = 0 # Rotación en X
y_angle = sp.pi / 2 # Rotación en Y (90°)
z_angle = sp.pi # Rotación en Z (180°)
# Calcular la matriz de rotación combinada
T_rotation = rotation_matrix(x_angle, y_angle, z_angle)
# Matriz total combinada
T_total = T_1 @ T_rotation @ T_2
# Mostrar la matriz de rotación y la matriz total, redondeado a 2 decimales
print("\nMatriz de rotación:")
sp.pprint(reemplazar_trigonometria(T_rotation)) # Redondear a 2 decimales
print("\nMatriz homogénea total T:")
sp.pprint(reemplazar_trigonometria(T_total)) # Redondear a 2 decimales
#Imprimir por columnas la matriz total
print("\n\n Columna 0")
sp.pprint(reemplazar_trigonometria(T_total).col(0))
print("\n\n Columna 2")
sp.pprint(reemplazar_trigonometria(T_total).col(1))
print("\n\n Columna 1")
sp.pprint(reemplazar_trigonometria(T_total).col(2))
print("\n\n Columna 3")
sp.pprint(reemplazar_trigonometria(T_total).col(3))
#Ejercicio 4
print("\nEjercicio 4:")
# Definir las variables simbólicas
th1, th2, th3, th4, th5, th6, d1, d2, d3, d4, d5, d6 = sp.symbols('th1 th2 th3 th4 th5 th6 d1 d2 d3 d4 d5 d6')
# Primera fila de la tabla DH: [α=-90, a=0, θ=th1, d=d1]
T1 = dh_matrix(th1, d1, 0, -sp.pi/2)
# Segunda fila de la tabla DH: [α=0, a=d2, θ=th2, d=0]
T2 = dh_matrix(th2, 0, d2, 0)
# Tercera fila de la tabla DH: [α=-90, a=0, θ=th3, d=d3]
T3 = dh_matrix(th3, d3, 0, -sp.pi/2)
# Cuarta fila de la tabla DH: [α=-90, a=0, θ=th4, d=d4]
T4 = dh_matrix(th4, d4, 0, -sp.pi/2)
# Quinta fila de la tabla DH: [α=90, a=0, θ=th5, d=0]
T5 = dh_matrix(th5, 0, 0, sp.pi/2)
# Sexta fila de la tabla DH: [α=0, a=0, θ=th6, d=d5]
T6 = dh_matrix(th6, d5, 0, 0)
# Matriz final: Producto de las transformaciones
T = T1 @ T2 @ T3 @ T4 @ T5 @ T6
# Mostrar las matrices individuales y el producto final, redondeado a 2 decimales
print("Matriz T1:")
sp.pprint(reemplazar_trigonometria(T1)) # Redondear a 2 decimales
print("\nMatriz T2:")
sp.pprint(reemplazar_trigonometria(T2)) # Redondear a 2 decimales
print("\nMatriz T3:")
sp.pprint(reemplazar_trigonometria(T3)) # Redondear a 2 decimales
print("\nMatriz T4:")
sp.pprint(reemplazar_trigonometria(T4)) # Redondear a 2 decimales
print("\nMatriz T5:")
sp.pprint(reemplazar_trigonometria(T5)) # Redondear a 2 decimales
print("\nMatriz T6:")
sp.pprint(reemplazar_trigonometria(T6)) # Redondear a 2 decimales
print("\nMatriz homogénea total T:")
sp.pprint(reemplazar_trigonometria(sp.simplify(T))) # Redondear a 2 decimales
# Ejercicio 5:
print("\nEjercicio 5:")
# Definir las variables simbólicas
th1, th2, th3, th4, th5, th6, d1, d2, d3, d4, d5, d6 = sp.symbols('th1 th2 th3 th4 th5 th6 d1 d2 d3 d4 d5 d6')
# Primera fila de la tabla DH: [α=-90, a=0, θ=th1, d=d1]
T1 = dh_matrix(th1, d1, 0, -sp.pi/2)
# Segunda fila de la tabla DH: [α=0, a=d2, θ=th2, d=0]
T2 = dh_matrix(th2, 0, d2, 0)
# Tercera fila de la tabla DH: [α=-90, a=0, θ=th3, d=d3]
T3 = dh_matrix(th3, d3, 0, -sp.pi/2)
# Cuarta fila de la tabla DH: [α=0, a=0, θ=th4, d=d4]
T4 = dh_matrix(th4, d4, 0, 0)
# Quinta fila de la tabla DH: [α=-90, a=0, θ=th5, d=d5]
T5 = dh_matrix(th5, d5, 0, -sp.pi/2)
# Sexta fila de la tabla DH: [α=0, a=0, θ=th6, d=d6]
T6 = dh_matrix(th6, d6, 0, 0)
# Matriz final: Producto de las transformaciones
T_1 = T1 @ T2 @ T3 @ T4
T_2 = T5 @ T6
# Juntar las matrices T1 y T2
x_angle = -(sp.pi / 2) # Rotación en X
y_angle = 0
z_angle = 0
# Calcular la matriz de rotación combinada
T_rotation = rotation_matrix(x_angle, y_angle, z_angle)
# Matriz total combinada
T = T_1 @ T_rotation @ T_2
# Mostrar las matrices individuales y el producto final, redondeado a 2 decimales
print("Matriz T1:")
sp.pprint(reemplazar_trigonometria(T1)) # Redondear a 2 decimales
print("\nMatriz T2:")
sp.pprint(reemplazar_trigonometria(T2)) # Redondear a 2 decimales
print("\nMatriz T3:")
sp.pprint(reemplazar_trigonometria(T3)) # Redondear a 2 decimales
print("\nMatriz T4:")
sp.pprint(reemplazar_trigonometria(T4)) # Redondear a 2 decimales
print("\nMatriz T5:")
sp.pprint(reemplazar_trigonometria(T5)) # Redondear a 2 decimales
print("\nMatriz T6:")
sp.pprint(reemplazar_trigonometria(T6)) # Redondear a 2 decimales
print("\nMatriz homogénea total T:")
sp.pprint(reemplazar_trigonometria(sp.simplify(T))) # Redondear a 2 decimales